由Otsu(大津展之)于1978年提出的最大类间方差法，是引起较多关注的一种阈值选取方法。它是在判决分析或最小二乘原理的基础上推导出来的。

 

参考文献：

[1] Otsu N. A threshold selection method from gray-level histogram. IEEE Trans,1979;SMC-9;62-66 

 

算法思想：

假设一幅图像有L个灰度级[1,2,…,L]。灰度级为i的像素点的个数为n_i，那么总的像素点个数就应该为N=n₁+n₂+…+n_L。为了讨论方便，我们使用归一化的灰度级直方图并且视为这幅图像的概率分布:

 

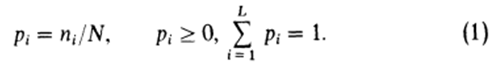
    现在假设我们通过一个灰度级为k的门限将这些像素点划分为两类:C₀和C₁(背景和目标,或者反之亦然)；C0表示灰度级为[1,…,k]的像素点，C1表示灰度级为[k+1,…,L]的像素点。那么，每一类出现的概率以及各类的平均灰度级分别由下面的式子给出：

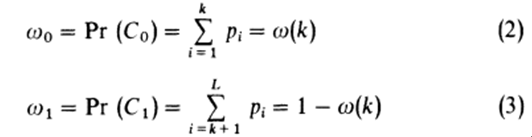
以及

其中，

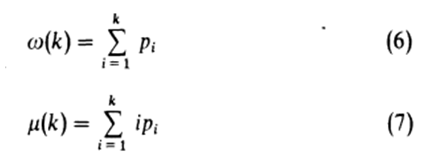
分别为灰度级从1到k的累积出现概率和平均灰度级（一阶累积矩），而

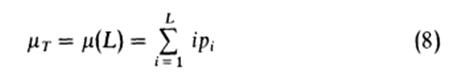
是整幅图像的平均灰度级。我们可以很容易验证，对于任意选定的k，都有：

这两类的类内方差由下面的公式给出：

这需要二阶累积矩(second-order cumulative moment，统计学概念)。

    为了评价(灰度级k)这个门限“好”的程度，我们需要引入判别式分析中使用的判别式标准来测量（类的分离性测量）：

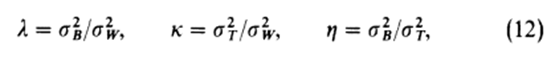
其中：

又根据式(9)，可以得出：

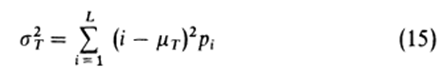
这三个式子分别是类内方差、类间方差和灰度级的总方差。然后，我们的问题就简化为一个优化问题，即寻找一个门限k使(12)式中给出的一个目标函数取最大值。

    这个观点是出于这样一个猜想，一个好的阈值将会把灰度级分为两类，那么反过来说，就是如果一个门限能够在灰度级上将图像分割为最好的两类的话，那么这个门限就是最好的门限。

    上面给出的判别式标准是分别求取λ、κ和η的最大值。然而，对于κ而言，它又等于另外一个，比如κ=λ+1；而对于λ而言，又有η=λ/(λ+1)，因为始终存在下面的基本关系：

  

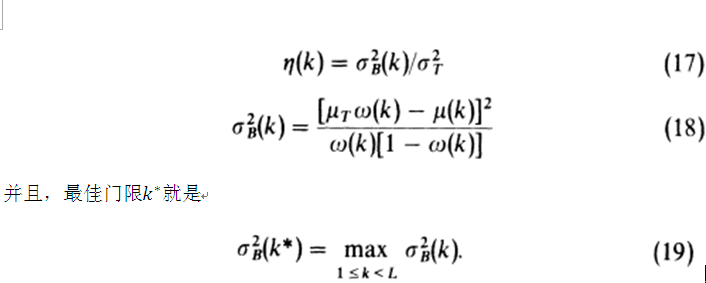
 效果展示：

 

 

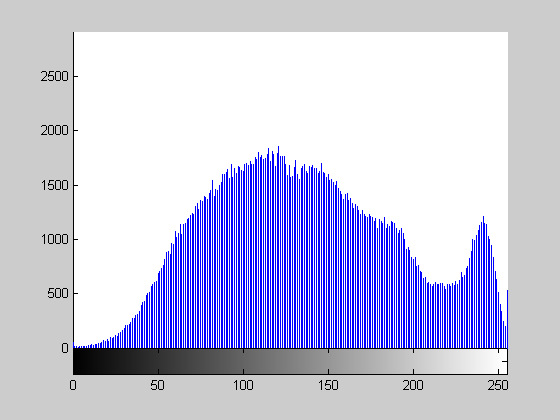
算法评价：

　　就最大类间方差算法而言，优点是算法简单，当目标与背景的面积相差不大时，能够有效地对图像进行分割。但是，当图像中的目标与背景的面积相差很大时，表现为直方图没有明显的双峰，或者两个峰的大小相差很大，分割效果不佳，或者目标与背景的灰度有较大的重叠时也不能准确的将目标与背景分开。导致这种现象出现的原因是该方法忽略了图像的空间信息，同时该方法将图像的灰度分布作为分割图像的依据，因而对噪声也相当敏感。所以，在实际应用中，总是将其与其他方法结合起来使用。